Analysis of Heat Dissipation Losses in High-Temperature Flanges and Pipelines Used in Oil Refineries
Abstract: High-temperature flanges and pipelines are critical components in oil refinery operations. Using a wax oil hydrocracking unit as a case study, this paper calculates and analyzes the heat dissipation losses of high-temperature reactor flanges and pipelines. The results indicate that accurate estimation of flange heat dissipation losses requires comprehensive consideration of both wind speed and the temperature difference between the flange surface and the surrounding environment. In addition, the presence or absence of thermal insulation has a significant impact on heat dissipation losses in pipelines. Based on the analysis, measures such as improving rainproof covers for high-temperature flanges and conducting regular maintenance of pipeline insulation are proposed to effectively reduce heat dissipation losses. High-temperature flanges and pipelines play a vital role in oil refinery systems, and an in-depth investigation of their heat dissipation behavior is essential for improving production efficiency and ensuring operational safety. Taking a typical wax oil hydrocracking unit as an example, this study evaluates the heat dissipation losses of high-temperature reactor flanges and pipelines and identifies the key factors influencing these losses. The findings provide a practical basis for reducing thermal losses and offer valuable references for energy conservation and reduced energy consumption in oil refineries.
The reaction system of the hydrocracking unit operates under high-temperature conditions, and thermal insulation is installed at most locations to minimize heat loss. However, the reactor inlet and outlet flanges are prone to leakage during temperature fluctuations associated with start-up and shutdown, as well as during pressure variations such as emergency depressurization. For ease of inspection and monitoring, these flanges are left uninsulated, resulting in unavoidable heat dissipation losses.
The heat dissipation loss of the equipment is calculated using the following equation:
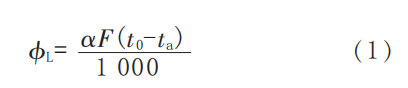
Where:
Q is the heat dissipation loss, in kW;
α is the overall heat transfer coefficient, in W/(m²·°C);
F is the external surface area of the equipment, in m²;
Ts is the surface temperature of the equipment, in °C;
Ta is the ambient temperature, in °C.
A reactor in the hydrocracking unit is equipped with two inlet elbow flanges, one large manhole flange, one manhole cover flange, and two outlet flanges. The relevant geometric dimensions of the reactor’s inlet and outlet flanges were obtained from the reactor design drawings and are listed in Table 1. The total external surface area of a flange is calculated as the sum of its bottom surface area, cylindrical surface area, and platform surface area:
Table 1 Dimensions of Reactor Inlet and Outlet Flanges (mm)
| Item | Inlet Elbow Flange | Inlet Cover Flange | Inlet Manhole Flange | Outlet Flange |
|---|---|---|---|---|
| Outer diameter of flange, Dₒ | 1340 | 1820 | 1820 | 1105 |
| Inner diameter of flange, Dᵢ | 490 | 490 | 915 | 408 |
| Overall flange height, H | 500 | 620 | — | 500 |
| Flange thickness, δ | 275 | 490 | 307 | 257 |
| Outer diameter of raised face, Dᵣ | 850 | 785 | — | 720 |
According to the secondary and tertiary test methods specified in SY/T 6421—1999, Determination of Heat Loss of Equipment and Pipelines, the overall heat transfer coefficient α\alphaα for ground-mounted equipment and pipelines can be calculated. For indoor thermal equipment and pipelines, where external wind effects are negligible, the overall heat transfer coefficients for flat and cylindrical surfaces can be calculated using Equations (6) and (7), respectively.
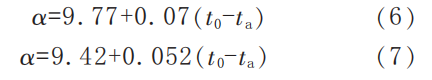
If the rain cover of the reactor flange in the hydrocracking unit is improved so that the entire flange surface is covered with aluminum sheet (without insulation), leaving only the inspection sealing surface exposed, the impact of wind and other external factors becomes negligible. In this case, the flange can be treated as an indoor installation, making Equation (7) applicable.
Field measurements with an infrared thermometer indicate that the surface temperatures of the reactor flanges are approximately as follows:
Inlet elbow flange: 214 °C
Inlet cover flange: 180 °C
Inlet manway flange: 223 °C
Outlet flange: 242 °C
The average annual ambient temperature at the equipment site is approximately 25 °C, ranging from a summer maximum of 40 °C to a winter minimum of 10 °C.
Taking the ambient temperature as Ta=25°C, and substituting Ts=214 °C into Equation (7), the overall heat transfer coefficient of the inlet elbow flange is calculated as:
a=19.25 W/(m2⋅°C)
Similarly, the overall heat transfer coefficients for the reactor inlet cover flange, inlet manway flange, and outlet flange are calculated to be 17.48, 19.71, and 20.70 W/(m²·°C), respectively.
For outdoor thermal pipelines and equipment, the overall heat transfer coefficient can be estimated using the following empirical equation:
a=11.63+7w0.5 (8)
where:
w is the wind speed in m/s.
The reactor flanges in the hydrocracking unit are all installed outdoors, with only their upper surfaces covered by rain shields. Consequently, they are strongly influenced by external wind, and the overall heat transfer coefficient of the flanges is calculated using Equation (8). The hydrocracking unit is situated in a coastal area where typical wind conditions range from Beaufort scale 2 to 4, corresponding to wind speeds of approximately 2–6 m/s for most of the year. In extreme weather, wind forces can exceed Beaufort scale 10, with speeds reaching up to 15 m/s. Taking a conservative wind speed of w=2 m/s, the overall heat transfer coefficient of the reactor flanges is calculated using Equation (8) as:
a=21.53 W/(m2⋅°C)
The overall heat transfer coefficient of the equipment is calculated using the following formula:
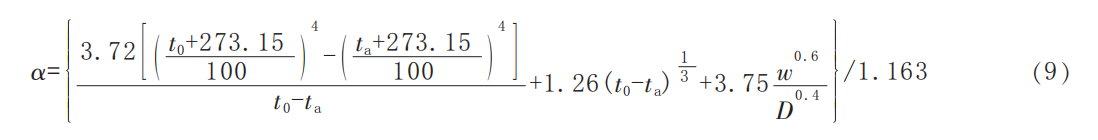
where:
a is the overall heat transfer coefficient, W/(m²·°C);
Ts is the equipment surface temperature, °C;
Ta is the ambient temperature, °C;
w is the wind speed, m/s;
D is the outer diameter of the heat-dissipating component, m.
Based on the annual wind conditions in the coastal region where the unit is located, the wind speed is taken as w=2 m/s.
Taking the reactor inlet elbow flange as an example, with Ts=214 °C, Ta=25 °C, and D=1.34 m, the overall heat transfer coefficient calculated using Equation (9) is:
a=18.76 W/(m2⋅°C)
Using the same calculation method, the overall heat transfer coefficients for the reactor inlet cover flange, inlet manhole flange, and outlet flange are 16.74, 18.67, and 20.42 W/(m²·°C), respectively.
Under a wind speed of w = 2 m/s, taking the reactor inlet elbow flange as a representative example, Calculation Method 3 yields an overall heat transfer coefficient of a = 18.76 W/(m²·°C) for the inlet elbow flange. With a flange surface temperature of Ts = 214 °C, an ambient temperature of Ta = 25 °C, and an external surface area of F = 5.98 m², substitution into Equation (1) gives a heat dissipation loss of 21.20 kW for the inlet elbow flange. Using the same calculation method, the heat dissipation losses of the inlet cover flange, inlet manhole flange, and outlet flange are 14.54 kW, 13.67 kW, and 19.77 kW, respectively, resulting in a total heat dissipation loss of 69.19 kW for all reactor flanges. To assess the accuracy of the heat transfer coefficients obtained from the three calculation methods and to analyze the effects of wind speed, flange surface temperature, and the temperature difference between the flange surface and the ambient environment on heat dissipation, the coefficients were calculated using Methods 1, 2, and 3. The heat dissipation losses of the reactor inlet and outlet flanges at different wind speeds were then calculated, and the results are compared in Figure 1.
Figure 1. Trends in heat dissipation losses of reactor inlet and outlet flanges at different wind speeds, calculated using three methods: Method 1 considers only the temperature difference, Method 2 considers only the wind speed, and Method 3 considers both factors.
A comparative analysis of Figure 1 reveals the following:
Calculation Method 1 considers only the effect of temperature difference. When the wind speed is below 2 m/s, its results are similar to those of Methods 2 and 3, which take wind effects into account.
Calculation Method 2 considers only the effect of wind speed. When the wind speed exceeds 4 m/s, its results differ significantly from those of the other two methods.
Calculation Method 3 comprehensively considers both wind speed and temperature difference. The resulting heat dissipation losses fall between those obtained using Methods 1 and 2, indicating higher accuracy and better applicability.
For calculating heat dissipation losses of outdoor high-temperature flanges, Equation (9) provides a more accurate and reliable estimation of the heat transfer coefficient. In coastal regions, where annual wind speeds typically range from 2 to 4 m/s, wind significantly influences heat dissipation, as illustrated in Figure 1. Therefore, although high-temperature flanges cannot be fully insulated, the rain cover should be optimized by covering the entire flange surface with aluminum sheeting (without insulation), leaving only the sealing surface exposed for inspection. This approach effectively mitigates the impact of external wind and environmental factors, thereby minimizing heat dissipation losses.
According to GB/T 19585—2012, Technical Specification for Pipeline Insulation Engineering, pipelines carrying media at temperatures above 60 °C must be insulated. Additionally, pipelines transporting media with densities greater than that of diesel should be equipped with heat tracing where required. At a hydrocracking unit site, a DN350 pipeline carrying the same process medium was observed to have partially damaged insulation, while the remaining sections remained intact. The pipeline was made of TP321 stainless steel, with an operating medium temperature of 350 °C and an internal pressure of 14.5 MPa. It had an outer diameter of 355.6 mm, a wall thickness of 31.7 mm, and an inner diameter of 292 mm. The insulation thickness was 130 mm, and the uninsulated section measured approximately 3 m in length. Field measurements indicated that the outer surface temperature of the uninsulated pipeline section was 213 °C, whereas the insulated section measured approximately 55 °C. The ambient temperature at the site was 30 °C.
The heat dissipation loss from the pipeline’s outer surface is calculated using the following equation:
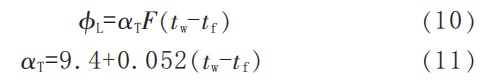
where:
Q is the heat loss, in kW;
α is the convective heat transfer coefficient, in W/(m²·°C);
F is the external surface area of the pipeline, in m²;
Ts is the pipeline outer surface temperature, in °C;
Ta is the ambient temperature, in °C.
The convective heat transfer coefficient for outdoor pipelines is calculated as:
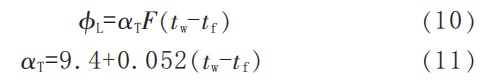
Where:
α is the convective heat transfer coefficient, W/(m²·°C)
Ts is the pipeline outer surface temperature, °C
Ta is the ambient temperature, °C
Assuming a wind speed of 1 m/s and substituting Ts=213 °C and Ta=30 °C into Equations (10) and (11), the heat dissipation loss of the uninsulated pipeline section is calculated to be 23.15 kW. If this pipeline section is insulated, the measured outer surface temperature decreases to Ts=55 °C. Substituting the corresponding values into Equations (10) and (11), the heat dissipation loss after insulation is reduced to only 1.79 kW.
When evaluating heat dissipation losses from flanges in high-temperature areas, it is essential to comprehensively consider the combined effects of wind speed, flange surface temperature, and the temperature difference between the flange surface and the ambient environment. Using a wax oil hydrocracking unit in a refinery as a case study, the heat dissipation losses of high-temperature flanges and pipelines at the reactor inlet and outlet were calculated and analyzed. At a wind speed of 2 m/s, the total heat dissipation from the reactor flanges is approximately 69.19 kW, representing a significant energy loss. From a safety perspective, high-temperature flanges in the field are generally left uninsulated, and local wind conditions have a significant impact on heat dissipation. Therefore, the rain covers on flanges in high-temperature areas should be enhanced by covering the entire flange surface with aluminum sheeting, leaving only the sealing surface required for inspection exposed. This approach effectively minimizes heat loss by reducing the impact of external wind and other environmental factors. For pipelines, comparing the same section with and without insulation shows heat losses of 1.79 kW and 23.15 kW, respectively, highlighting a substantial reduction when insulation is applied. Consequently, regular inspection and maintenance of insulation layers on high-temperature pipelines in refinery units are essential to ensure their integrity, minimize energy losses, and maintain safe and efficient operation.
Related News
- Structural Design and Strength Analysis of a Deepwater Riser Suspension Flange
- Analysis of Heat Dissipation Losses in High-Temperature Flanges and Pipelines Used in Oil Refineries
- Failure and Crack Analysis of an EO/EG Unit Tower Inlet Flange
- Pipe Flange Bolt Tightening in LNG Projects: Key Considerations
- Ultrasonic Testing of High-Neck Flange Welds
- Underwater Flange Connection Methods for Submarine Pipelines
- Key Technologies for Pressure Vessel Testing and Flange Connection Design
- Installation of Main Bolts for Lap Joint Flange in High-Temperature Gas-Cooled Reactors
- Structural Design and Finite Element Analysis of Anchor Flanges
- Key Welding Technology for High-Neck Flange and Steel Pipe Joints
